Rate-Independent Ineslatic formulation
Stress-strain curve
In uniaxial tension tests of most metals (and many other materials), the following phenomena can be observed. If the stress in the specimen is below the yield stress of the material, the material behaves elastically and the stress in the specimen is proportional to the strain. If the stress in the specimen is greater than the yield stress, the material no longer exhibits elastic behavior, and the stress-strain relationship becomes nonlinear. Figure below shows a typical uniaxial stress-strain curve. Both the elastic and inelastic regions are indicated.
Within the elastic region, the stress-strain relationship is unique. As illustrated in next figure, if the stress in the specimen is increased (loading) from zero (point 0) to (point 1), and then decreased (unloading) to zero, the strain in the specimen is also increased from zero to 
, and then returned to zero. The elastic strain is completely recovered upon the release of stress in the specimen.
The loading-unloading situation in the inelastic region is different from the elastic behavior. If the specimen is loaded beyond yield to point 2, where the stress in the specimen is σ2 and the total strain is 2, upon release of the stress in the specimen the elastic strain, 
, is completely recovered. However, the inelastic (plastic) strain, 
, remains in the specimen.
Similarly, if the specimen is loaded to point 3 and then unloaded to zero stress state, the plastic strain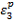 
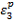remains in the specimen. It is obvious that is not equal to . We can conclude that in the inelastic region:
-
Plastic strain permanently remains in the specimen upon removal of stress.
-
The amount of plastic strain remaining in the specimen is dependent upon the stress level at which the unloading starts (path-dependent behavior).
The uniaxial stress-strain curve is usually plotted for total quantities (total stress versus total strain). The total stress-strain curve can be replotted as a total stress versus plastic strain curve, as shown in the next figure which shows the definition of workhardening slope (Uniaxial Test). The slope of the total stress versus plastic strain curve is defined as the workhardening slope (H) of the material. The workhardening slope is a function of plastic strain.
The stress-strain curve shown is directly plotted from experimental data. It can be simplified for the purpose of numerical modeling. A few simplifications are shown in next figures and are listed below:
-
Bilinear representation – constant workhardening slope
-
Elastic perfectly-plastic material – no workhardening
-
Perfectly-plastic material – no workhardening and no elastic response
-
Piecewise linear representation – multiple constant workhardening slopes
-
Strain-softening material – negative workhardening slope
In addition to elastic material constants (Young’s modulus and Poisson’s ratio), it is essential to include yield stress and workhardening slopes when dealing with inelastic (plastic) material behavior. These quantities can vary with parameters such as temperature and strain rate. Since the yield stress is generally measured from uniaxial tests, and the stresses in real structures are usually multiaxial, the yield condition of a multiaxial stress state must be considered.
The conditions of subsequent yield (workhardening rules) must also be studied.
Yield Conditions
The yield stress of a material is a measured stress level that separates the elastic and inelastic behavior of the material.
The magnitude of the yield stress is generally obtained from a uniaxial test. However, the stresses in a structure are usually multiaxial. A measurement of yielding for the multiaxial state of stress is called the yield condition. Depending on how the multiaxial state of stress is represented, there can be many forms of yield conditions. For example, the yield condition can be dependent on all stress components, on shear components only, or on hydrostatic stress.
Von Mises yield condition
Although many forms of yield conditions are available, the von Mises criterion is the most widely used. The success of the von Mises criterion is due to the continuous nature of the function that defines this criterion and its agreement with observed behavior for the commonly encountered ductile materials. The von Mises criterion states that yield occurs when the effective (or equivalent) stress 
equals the yield stress 
as measured in a uniaxial test.
Figure below shows the von Mises yield surface in two-dimensional and three-dimensional stress space.
For an isotropic material:
Where 
and 
are the principal Cauchy stresses.
can also be expressed in terms of nonprincipal Cauchy stresses.
The yield condition can also be expressed in terms of the deviatoric stresses as:
where 
is the deviatoric Cauchy stress expressed as
For isotropic material, the von Mises yield condition is the default condition in CivilFEM.
