|
|||||
 Analysis button
Material constitutive law for analysis
Concrete
CivilFEM has the option of choosing the analysis type in order to define the material behavior that the program will use during the solving process. Concrete analysis type can be chosen between both linear and short term loads diagram.
Linear
The linear elastic model is the most commonly used model to represent typical engineering materials. This model, that showcases a linear relationship between stresses and strains, is represented by Hooke’s Law. The figure below shows that stresses are proportional to strains in a uniaxial tension test. The ratio of stress to strain is the familiar definition of modulus of elasticity (Young’s modulus) of the material.
E (modulus of elasticity) = (axial stress)/(axial strain)
Linear analysis has the characteristic of not limiting the strain while stresses increase.
We could say that a linear diagram does not follow the real material behavior. However, this diagram is very useful if the user wants to perform an analysis in the linear stages of the material and doesn't need a more detailed but slower non-linear calculation.
If the user does not choose a particular analysis type, CivilFEM will apply a linear analysis by default.
Short term loads diagram
CivilFEM has three options for non-linear behaviour when choosing a short term loads diagram on the Constitutive law Analysis of concrete: Buyukozturk plasticity, multilinear elastic and nonlinear isotropic hardening. These material models offer three different advanced concrete plasticity options for fine tuning critical concrete simulations.
Buyukozturk plasticity
CivilFEM includes the Buyukuzturk plasticity model for the prediction of yield and failure of concrete under combined stress. The model takes into account two sources of nonlinearity: progressive cracking of concrete in tension and the nonlinear response of concrete under multiaxial compression.
The representation of this model is shown in the following picture:
This failure law for concrete is used:
The law becomes:
Multilinear elastic
This option allows the input of simplified nonlinear elastic models that do not have a well defined strain energy function. It allows an easy way to represent behavior that can be gathered from real world material tests. The theory and algorithms are adequate to define the stress-strain curve accurately for uniaxial loading cases.
This is the graph that represents the material behavior in a multilinear elastic material:
The nonlinear elastic capability satisfy the equivalence of the deformation work per unit volume in the simple tension to the strain energy per unit volume, while the work done for deformation may be defined by a stress-strain curve in simple tension.
The effective strain ε may be defined ahead:
From the total differential of the above equation, the next one is obtained:
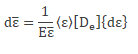
Substituting the latter in the first equation above:
The
 1 parameter in the graph, correspond to the first slope for which the first elasticity module, in relation with the curve, is required. The E parameter is not a constant thorough the curve.
The
 is assumed as a value from which the graph takes a constant value for σ, approaching to 0.1, the maximum value for strain.
Isotropic plasticity model
This criterion is suitable for the most common ductile materials. The model states that yield occurs when the effective (or equivalent) stress
 equals the yield stress  as measured in a uniaxial test.
The yield surface of the model in two-dimensional and three-dimensional stress space will be shown below .
For an isotropic material:
The yield condition can also be expressed in terms of the deviatoric stresses as:
The yield condition can also be expressed in terms of the deviatoric stresses as:
Drucker-Prager
Otherwise, a Drucker-Prager analysis is available for concrete material.
If the user activates the Drucker-Prager option, two new parameters are showed: the effective cohesion and the effective internal friction angle.
Variable cohesion, depending on the equivalent plastic strain, can be defined by just clicking the checkbox:
 
A more detailed description about the Drucker Prager analysis will be provided both in the rocks and soils constitutive laws.
|
