|
|||||
 Behavior button
Material constitutive law for analysis
CivilFEM has the option of choosing the analysis type in order to define the material behavior that the program will use during the solving process. Available material models would be: Linear Elastic, Drucker-Prager, Mohr-Coulomb, Cam clay, NonLinear Elastic, Hyperbolic and Small-strain brick.
Linear Elastic
The linear elastic model is the most commonly used model to represent typical engineering materials. This model, that showcases a linear relationship between stresses and strains, is represented by Hooke’s Law. The figure below shows that stresses are proportional to strains in a uniaxial tension test. The ratio of stress to strain is the familiar definition of modulus of elasticity (Young’s modulus) of the material.
E (modulus of elasticity) = (axial stress)/(axial strain)
Linear analysis has the characteristic of not limiting the strain while stresses increase.
We could say that a linear diagram does not follow the real material behavior. However, this diagram is very useful if the user wants to perform an analysis in the linear stages of the material and doesn't need a more detailed but slower non-linear calculation.
If the user does not choose a particular analysis type, CivilFEM will apply a linear analysis by default.
Drucker-Prager
CivilFEM includes options for elastic-plastic behavior based on a yield surface that exhibits hydrostatic stress dependence. Such behavior is observed in a wide class of soil and rock-like materials. These materials are generally classified as Mohr-Coulomb materials (generalized von Mises materials). The generalized Mohr-Coulomb model developed by Drucker and Prager is implemented in CivilFEM.
The yield function for the Drucker-Prager criterion is:
   
In CivilFEM the parameters
 and  are expressed in function of the cohesion c and the angle of internal friction  .
With these values for c and
 parameters the Drucker-Prager surface represents an outer bond cone of the Mohr-Coulomb hexagonal pyramid.
Drucker-Prager analysis implemented in CivilFEM follows the Rate-Independant Ineslastic behaviour formulation, which has been specified in the corresponding annex.
Mohr-Coulomb
CivilFEM includes a modified version of Mohr-Coulomb model described in [1] to correct for singularities at apex and edges of the yield surface.
The yield condition is expressed as:
Where
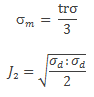
Being
 the deviatoric part of stress tensor  .  is the friction angle, hyp is a parameter that controls the rounding of the yield surface at the apex, and K is a function that smoothes the yield surface in the deviatoric plane.
This modified version of Mohr-Coulomb model, asymptotically approximates the standard form. Hyp is the distance between the apex of the standard and the modified yield surfaces. For hyp>0 the modified surface is smooth at the apex; for hyp=0, the modified surface matches the standard form at the apex, and the singularity will be restored at this point.
A value of:
provides an excellent approximation [1], this is the default value used by CivilFEM.
The function has the form:
being
 the Lode angle defined by  is the transition angle where the corners of the deviator plane are rounded. CivilFEM uses a value of 25° which provides sufficient approximation, this value cannot be modified by the user. Parameters A and B are determined by
Deviatoric section
 
The constitutive law is that of a linear elastic and isotropic material. In case of small displacements this law is expressed as:
where C is the elasticity tensor,
 is the total strain tensor, and  is the plastic strain tensor.
When geometric nonlinearity is active the constitutive law is entirely analogue to the geometrically linear case but using the second Piola-Kirchhoff stress and the Green-Lagrange strain tensors
so this formulation implicitly assumes that stretches are small. In particular, as in an elastic material, material instability can arise by large compressive strains.
Except by the stress and strains tensors both geometrically linear and nonlinear cases are equivalent. Although everything said is referred to the linear case also it is applicable to the nonlinear case.
In regard to the hardining law, it is noticeable that the current version of Mohr-Coulomb model does not support hardening.
The flow rule in Mohr-Coulomb model is defined by:
Where g is the plastic potential that has the same expression as f except that the friction angle is replaced by the dilatancy angle when flow is not associated.
Mohr-Coulomb analysis implemented in CivilFEM follows the Rate-Independant Ineslastic behaviour formulation, which has been specified in the corresponding annex.
Input data
Mohr-Coulomb model is only available for soils and rocks. The material properties and parameters that define the model are shown below:
For associated flow, it is not necessary to provide the dilatancy. A null value for cohesion is not admitted, therefore for non-cohesive materials a small value must be introduced.
[1] A.J. Abbo And S. W. Sloan, A Smooth Hyperbolic Approximation to the Mohr-Coulomb Yield Criterion, Computers & Structures, Vol. 54, No. 3, pp. 427-441 (1995).
Cam-Clay
The version of Cam-clay model implemented in CivilFEM is an extension of the modified Cam-clay (Roscoe and Burland, 1968) since it supports stress states with tensile components. This model is described in [2] and the yield condition is defined by
where
  is the deviatoric part of stress tensor  , a is a parameter that controls the size of the surface along the pressure axis, M is the slope of the critical state line (CSL) and  is the tensile yield hydrostatic stress. The parameter b takes the form
being
 a material constant. This parameter modifies the length of the axis on the right part of the yield surface. When  both halves of the yield surface are equal and the yield condition coincides with that of standard Cam-clay. From the figure below the following relation is obtained  
The constitutive law is that of a linear hypoelastic and isotropic material. In case of small displacements this law is expressed as
Where C is the material tensor and corresponds to the standard elasticity tensor of a linear and isotropic material,
is the total strain tensor, and is the plastic strain tensor. The material tensor depends of the stress state. In the present formulation is assumed that the Poisson ratio  is constant and that the bulk modulus  varies according to the law:
where
 is the specific volume of the material (ratio between the total volume and the volume of the solid part, that is, excluding the volume occupied by fluid), and  is the slope of the unloading-reloading line (URL) also known as swelling line.
When geometric nonlinearity is active the constitutive law is entirely analogue to the geometrically linear case but using the second Piola-Kirchhoff stress and the Green-Lagrange strain tensors
so this formulation implicitly assumes that stretches are small. In particular, as in an elastic material, material instability can arise by large compressive strains.
Except by the stress and strains tensors both geometrically linear and nonlinear cases are equivalent. Although everything said is referred to the linear case also it is applicable to the nonlinear case.
The hardening law implies that the size of the yield surface is controlled by the consolidation pressure that follows this evolution law:
where the specific volume is computed from
being
 the initial specific volume.
Another rule is the flow rule, that in decoupled form is:
 
where
 is the plastic multiplier.
Cam-Clay analysis implemented in CivilFEM follows the Rate-Independant Ineslastic behaviour formulation, which has been specified in the corresponding annex.
Computation of a consistent initial state
In the Cam-clay model is necessary to set up an initial state of consolidation which is computed from an initial stress state and an initial preconsolidation defined by the user. When the initial stress state is inside of the yield surface the material response is elastic: over consolidated state; but if the initial stress state is onto yield surface, the response will be plastic: normal-consolidation state. Since an initial state external to the yield condition is not physically possible, the program will modify the value of the preconsolidation pressure provided
 by the user so that the initial state is normal-consolidated or elastic. The procedure followed is described below:
1. Define an initial preconsolidation pressure
 and an initial stress tensor 
2. Compute a value of the initial preconsolidation pressure
 such that  
3. Recompute the initial value of the preconsolidation pressure as:
 .
4. Compute an initial value of the specific volume consistent with the material constants provided:
Input data
The data needed to define a Cam-clay are the following:
CSL =Critical state line
ICL = isotropic compression line
URL = unloading – reloading (sweling line)
Assumptions and restrictions
[2] E. A. de Souza Neto, D. Peric, D. R. J. Owen. Computational Methods for Plasticity. Wiley (2008).
Non Linear Elastic
This material model is based on the document The Sandia GeoModel: Theory and User's Guide, referenced by SAND2004-3226. This study has been developed in the Sandia National Laboratories.
This GeoModel supports the nonlinear elasticity by permitting the elastic tangent module to vary with the stress, according to the formulation ahead:
 
Where:
b0: initial elastic bulk modulus.
b1: high pressure coefficient in nonlinear elastic bulk modulus function. For linear elasticity b1=0.
b2: curvature parameter in nonlinear elastic bulk modulus function. For linear elasticity, b2= 0.
g0: initial elastic shear modulus.
g1: parameter used to define the elastic shear modulus at large shears.
g2: curvature parameter in nonlinear elastic shear modulus function.
I1: first stress invariant.
J2: second stress invariant
The bk and gk parameters are material constants determined via nonlinear regression fitting to the unloading portions of hydrostatic compression and triaxial compression experiments.
The equation coefficients have to fulfill some numerical limits in order to provide of consistency to the mode. These Nevertheless, the reference (SAND2004-3226) previously descried content a more detailed description about this topic. In addition, this table pretends to summarize those numerical limits but also the parameter units.
For a more extended information about the Sandia Geomodel, check the reference (SAND2004-3226) previously described.
Hyperbolic
The Duncan Chang model may be catalogued into two different frames, due to the fact that Poisson´s coefficient can be either constant or variable.
The constitutive law would be the one of a isotropic and nonlinear elastic material. In case of small displacements, the law would be defined as follows:
On the other hand, the elastic modulus load step will be calculated by means of the equation described ahead:
Where if
   , the formulation will take -0.01Pa. The same equation shows that in case:
The elastic modulus value would be null. However, this tension value will be never reached due to the compression resistance:
Thus, the elasticity modulus, in load step, will be calculated depending on two conditions. The first will be applied in case
 while the second is applied when  : 
The alpha coefficient is defined as the reduction factor of the elasticity modulus once the compression resistance has been exceeded. As a result of this explanation, the next table tries to gather a description of the coefficients which are necessary for CivilFEM in order to apply this material model:
By last, it becomes useful to add that elastic modulus equation in the loading-unloading step will be defined as:
In case the model situation has been carried out by means of a variable Poisson coefficient, the volumetric modulus is obtained ahead:
The K coefficient calculation is not affected neither the loading nor the unloading step.
Small-strain brick
This model is based in [1] which is a refinement of the small-strain overlay material model [3].
The S shaped characteristic stiffness-strain shows that the elastic modulus of soil is dependent on the level of shear strain.
In this model the dependency of the shear modulus with the strain is related with a variable that can be assumed as a equivalent shear strain:
The formula for the shear modulus is:
where:
and g is a function that includes the influence of the stress.
[1] M. Cudny, A. Truty. Refinement of the Hardening Soil model within the small strain range, Acta Geotechnica15:2031–2051 (2020).
[3] T. Benz, P.A. Vermeer, R. Schwab. A small-strain overlay model, Int. J. Numer. Anal. Meth. Geomech. 33:25-44(2009).
| |||||||||||||||||||||||||||
