Concrete Material

Concrete General Properties:

General properties are those properties common to all concrete materials. These properties have labels and values described here after:

Concrete General Properties
Name	Material name
Type	Concrete
ν	Poisson ratio () Default value depends on the active code: ν = 0.2 Eurocode 2 (Art 3.1.2.5.3) ν = 0.2 ACI 318 (Art 116R-45) ν = 0.2 CEB-FIP (Art 2.1.4.3) ν = 0.2 EHE (Art 39.9) ν = 0.2 BS 8110 (Art 2.4.2.4) ν = 0.2 Australian Standard 3600 ν = 0.2 GB 50010 ν = 0.2 NBR 6118 ν = 0.2 AASHTO Standard Specifications for H. B. ν = 0.2 Indian Standard 456 ν = 0.2 Cπ 52-101-03 ν = 0.2 ITER Structural Design Code for Buildings
ρ	Density
Act. time	Activation time
Deact. time	Deactivation time
G	Shear modulus. Is calculated using the formula:
α	Coefficient of linear thermal expansion Default value depends on the active code: α = 1.0E-5 (ºC^-1) Eurocode 2 (Art 3.1.2.5.4) α = 1.0E-5 (ºC^-1) ACI 318 (Art 116R-45) α = 1.0E-5 (ºC^-1) CEB-FIP (Art 2.1.8.3) α = 1.0E-5 (ºC^-1) EHE (Art 39.10) α = 1.0E-5 (ºC^-1) BS 8110 (Part 2: 7.5) α = 1.0E-5 (ºC^-1) Australian Standard 3600 α = 1.0E-5 (ºC^-1) GB 50010 α = 1.0E-5 (ºC^-1) NBR 6118 α = 1.0E-5 (ºC^-1) AASHTO Standard Spec. for H. B. α = 1.0E-5 (ºC^-1) Indian Standard 456 α = 1.0E-5 (ºC^-1) Cπ 52-101-03 α = 1.0E-5 (ºC^-1) ITER Structural Design Code for Buildings
Damping	Damping properties

Concrete Specific Properties:

Concrete Specific Properties
Ex Type	Type of elastic modulus used for linear analysis: Tangent modulus of elasticity Initial modulus of elasticity Secant modulus of elasticity Design modulus of elasticity Reduced modulus of elasticity User defined modulus of elasticity
Linear Ex	Modulus of elasticity for linear analysis. The different options for the elastic modulus will vary depending on the active code: Eurocode 2 Linear Ex = Ecm (default), Ec, Ecd ACI 318 Linear Ex = Ec (default) CEB-FIP Linear Ex = Ec (default), Eci, Ec1 EHE Linear Ex = Ej (default), Eci, Ec0 BS 8110 Linear Ex = Ec (default) Australian Standard 3600 Linear Ex = Ec (default) GB 50010 Linear Ex = Ec (default) NBR 6118 Linear Ex = Ecs (default), Eci AASHTO Standard Spec. for H. B. Linear Ex = Ec (default) Indian Standard 456 Linear Ex = Ec (default) Cπ 52-101-03 Linear Ex = Eb (default) ITER Structural Design Code for Buildings Linear Ex = Ecm (default), Ec, Ecd
Ages	Ages defined for the concrete time dependent properties (maximum of 20 age values). Default values: 1, 3, 7, 10, 14, 21, 28, 40, 60, 75, 90, 120, 200, 365, 600, 1000, 1800, 3000, 6000, 10000 days
Analysis σ-ε diagram	Analysis stress-strain diagram. Each different type of stress-strain diagrams available depends on the code for which the material was defined. Apart from available diagrams supported by the codes, it is possible to define new diagrams by changing the table data. SAε: Strain values corresponding to a point of the diagram. SAσ: Stress values corresponding to a point of the diagram.
Design σ-ε diagram	Design stress-strain diagram. Each different type of stress-strain diagrams available depends on the code for which the material was defined. Apart from available diagrams supported by the codes, it is possible to define new diagrams by changing the table data. SDε: Strain values corresponding to a point of the diagram. SDσ: Stress values corresponding to a point of the diagram.
ε min	Maximum admissible strain in compression at any point of the section (Point B of the pivots diagram) Sign criterion: + Tension, - Compression Eurocode 2 ε min = - 0.0035 If concrete has fck > 50 MPa, then ε min = -(2.6+35[(90-f_ck)/100]⁴) · 10^-3 (f_ck in MPa) ACI 318 ε min = - 0.0030 CEB-FIP Maximum admissible strains depend on the selected stress-strain diagram: ε min = - 0.0035 (User defined σ-ε diagram) ε min = - ε cuB (Parabolic rectangular σ-ε diagram) ε min = - ε cuU (Uniform stress σ-ε diagram) EHE ε min = - 0.0035 If concrete has fck > 50 MPa, then ε min = -(2.6+14.4[(100-f_ck)/100]⁴) · 10^-3 (f_ck in MPa) BS 8110 ε min = - 0.0035 GB 50010 ε min = ε cu NBR 6118 ε min = - 0.0035 Indian Standard 456 ε min = - 0.0035 Cπ 52-101-03 ε min = ε b2
ε int	Maximum allowable strain in compression at internal points of the section (Point C of the pivot diagram) Sign criterion: + Tension, - Compression Eurocode 2 ε int = - 0.0020 If concrete has fck > 50 MPa, then ε int = -(2.0+0.085(f_ck-50)^0.53) · 10^-3 (f_ck in MPa) ACI 318 ε int = 0 (No limit) CEB-FIP Maximum admissible strains depend on the selected stress-strain diagram ε int = - 0.0020 (User defined σ-ε diagram) ε int = - ε cuC (Parabolic rectangular σ-ε diagram) ε int = 0 (No limit) EHE ε int = - 0.0020 If concrete has fck > 50 MPa, then ε int = -(2.0+0.085(f_ck-50)^0.5) · 10^-3 (f_ck in MPa) BS 8110 ε int = 0 (No limit) GB 50010 ε int = ε 0 NBR 6118 ε int = - 0.0020 Indian Standard 456 ε int = - 0.0020 Cπ 52-101-03 ε int = ε b0
PCLevel	Ratio of the height of the section from the most compressed face at which point C is located: PCLevel = 3/7 (default value)

Concrete Specific Code Properties

There are some properties in CivilFEM that are code dependent. Code dependent properties are described hereafter for concrete materials supported by CivilFEM.

Concrete σ-ε diagrams
Codes	Analysis σ-ε diagram	Design σ-ε diagram
EC2_08, EC2_91, ITER, EHE-98 y EHE-08, CEB-FIP	Short term loads	Parabolic-rectangular Bilinear
BS8110	Structural Analysis	Parabolic-rectangular
NBR6118		Parabolic-rectangular
IS456		Parabolic-rectangular
GB50010	Structural Analysis	Parabolic-rectangular
Cπ 52101	Bilinear Trilinear	Bilinear Trilinear
ACI318, ACI349, ACI359, AS3600 and AASHTOHB	Parabolic-rectangular	Parabolic-rectangular

1. Eurocode 2 (Concrete) Properties

For this code, the following properties are considered:

Eurocode 2 Concrete Properties
βcc	Coefficient which depends on concrete age. Used to calculate time-dependant properties: βcc = exp {s·[1-(28/Age)^1/2]} (Age in days)
γc	Partial safety factor. γc = 1.5 (default value)
εc1	Strain of the peak compressive stress. Default values: εc1= -0.0022 for Eurocode 2 1991 and fck 50MPa εc1= 0.7·fcm0.31 < 2.8 for Eurocode 2 2008 (- Compression)
εcu	Ultimate strain in compression (- Compression)
fck	Characteristic compressive strength. Depends on concrete age: fck_t = fcm_t - 8 (fck_t and fcm in MPa) (+ Compression)
fcd	Design compressive strength. Depends on concrete age: fcd_t = fck_t/ γc (+ Compression)
fcm	Mean compressive strength. Depends on concrete age: fcm_t = βcc *fcm_28-day (+ Compression)
fctm	Mean tensile strength: (+ Tension) fctm = 0.3· (fck_28-day ^2/3) if fck 50 Mpa (fctm, fcm and fctk in MPa) fctm = 2.12·ln(1+(fcm_28-day /10)) if fck > 50 MPa
fctk005	Lower characteristic tensile strength (percentile-5%) fctk005 = 0.7·fctm (+Tension)
fctk095	Upper characteristic tensile strength (percentile-95%) fctk095 = 1.3·fctm (+Tension)
Ecm	Secant modulus of elasticity. Depends on concrete age: Ecm = 9500· [(fck_t+8)^1/3] (fck_t and Ecm in MPa)
Ec	Tangent modulus of elasticity. Depends on concrete age: Ec = 1.05·Ecm
Ecd	Design modulus of elasticity. Depends on concrete age: Ecd = Ecm/ γc
Cement type	Refers to the different types of cement used: S: Slow hardening cements N: Slow hardening cements (Default value) R: Rapid hardening cements RS: Rapid hardening high strength cements

Stress-Strain Diagrams for Structural Analysis

The different types of stress-strain diagrams available for concrete, according to Eurocode 2 are the following:

User defined
Elastic
Short-term loads

a) Definition of the elastic stress-strain diagram.

The sign criterion for the definition of stress-strain diagram points is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 2 points has been selected for the definition of the stress-strain diagram. Strain values are the following:

SAε (1)= -10^-2
SAε (2)= 10^-2

For these points, stress values are the following:

SA σ (i) = SAε (i) · Ex

b) Definition of the stress-strain diagram for short term loads

The sign criterion for the definition of stress-strain diagram points is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 20 points has been chosen for the definition of the stress-strain diagram. The strain values are the following:

SAε (1)= 1.000 · (εcu-εc1)+ εc1
SAε (2)= 0.793 · (εcu-εc1)+ εc1
SAε (3)= 0.617· (εcu-εc1)+ εc1
SAε (4)= 0.468· (εcu-εc1)+ εc1
SAε (5)= 0.342· (εcu-εc1)+ εc1
SAε (6)= 0.234· (εcu-εc1)+ εc1
SAε (7)= 0.143· (εcu-εc1)+ εc1
SAε (8)= 0.066· (εcu-εc1)+ εc1
SAε (9)= 1.000 · εc1
SAε (10)= 0.964· εc1
SAε (11)= 0.922· εc1
SAε (12)= 0.873· εc1
SAε (13)= 0.816· εc1
SAε (14)= 0.749· εc1
SAε (15)= 0.669· εc1
SAε (16)= 0.575· εc1
SAε (17)= 0.465· εc1
SAε (18)= 0.335· εc1
SAε (19)= 1.181· εc1
SAε (20)= 0.000

For these points, stress values are the following:

SA σ_(i) = -[(k*Eta_(i) -Eta_(i) ²)/((1+(k-2) ·Eta_(i))] ·fcm_t

K =

1.10·Ecm·EPSc1/(-fcm_t) for Eurocode 2 1991

1.05·Ecm·EPSc1/(-fcm_t) for Eurocode 2 2008

Eta_(i)= SAε_(i) / SAε c1

Stress-Strain Diagrams for Section Analysis

The different types of stress-strain diagrams available for concrete, according to Eurocode 2 are the following:

User defined
Parabolic-rectangular
Bilinear

a) Definition of the parabolic-rectangular stress-strain diagram:

Number of diagram points = 12

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain values for this diagram are the following:

SDε (1)= _cu2
SDε (2)=_c2
SDε (3)= 0.9 · _c2
SDε (4)= 0.8 · _c2
SDε (5)= 0.7 · _c2
SDε (6)= 0.6 · _c2
SDε (7)= 0.5 · _c2
SDε (8)= 0.4 · _c2
SDε (9)= 0.3 · _c2
SDε (10)= 0.2 · _c2
SDε (11)= 0.1 · _c2
SDε (12)= 0.0

Where:

_cu2 = -0.0035 if fck 50 MPa

_cu2 = -(2.6+35[(90-fck)/100]⁴)/1000 if fck > 50 MPa

_c2 = - 0.0020 if fck 50 MPa

_cu2 = -(2.0+0.085(fck-50)^0.53)/1000 if fck > 50 MPa (fck in MPa)

The corresponding stress values are the following:

For the first 11 points:

SD σ_(i) = 1000*SD_(i) · (250*SD_(i) +1) ·ALP·fcd_t for Eurocode 2 1991

SD σ_(i) = -[1-(1-SD_(i) / _c2)ⁿ] ·ALP·fcd_t for Eurocode 2 2008

n = 2.0 for fck 50 MPa

n = 1.4+23.4· [(90-fck)/100]⁴ for fck > 50 MPa

For point 12:

SDSGM_(i) = -ALP·fcd_t

b) Definition of the bilinear diagram

Number of diagram points = 3

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 3 points has been chosen for the definition of the stress-strain diagram. Strain values conform to article Art. 4.2.1.3.3 (b) of Eurocode 2 and are the following:

SD (1)= _cu3
SD (2)= _c3
SD (3)= 0.000

Where

_cu3 = -0.0035 for fck 50 MPa

_cu3 = -0.001· (2.6+35*[(90-fck)/100]⁴) for fck > 50 MPa

_c3 = -0.00135 for fck 50 MPa and Eurocode 2 1991

_c3 = -0.00175 for fck 50 MPa and Eurocode 2 2008

_c3 = -0.001· (1.75+0.55*(fck-50)/40) for fck > 50 MPa

Stress points are the following:

SD σ (1)= -ALP·fcd_t
SD σ (2)= -ALP·fcd_t
SD σ (3)= 0.000

2. ACI 318-05 (Concrete) Properties

ACI 318-05 Concrete Properties

Characteristic compressive strength (ACI-209R-4 Art. 2.2.1)

Depends on concrete age:

fc_t = Age / (a+ ß1·Age) ·fc_28-day (+ Compression)

Modulus of rupture (ACI-318 Art. 9.5.2.3). Depends on concrete age:

fr·7.5*fc_t^1/2

Elastic modulus (Art. 8.5.1 of the ACI-318). Depends on concrete age:

Ec = Wc^1.5·33·fc_t^1/2/ Wc 155 (Wc in lb/ft³)

Cement type

Cement type:

I: cement type I (default value)

III: cement type III

Curing type

Curing type:

MOIST: moist cured (default value)

STEAM: steam cured

ß1

Factor to transform the parabolic stress distribution of the beam compressive zone to a rectangular one (Art. 10.2.7.3 of the ACI-318). This factor 1 varies depending on the concrete characteristic strength. The different values this factor may have are described below:

fc
fc 4000 psi	0.85
8000 psi > fc > 4000 psi	0.85 - 0.05· (fc-4000)/1000
fc 8000 psi	0.65

Note: All these formulae are valid for fc of 28 days.

Strain of the peak compressive stress for parabolic stress-strain diagram. (Parabolic Stress strain diagram provided by PCA).

0= 2· (0.85·fc_t)/Ec (+ Compression)

Stress-Strain Diagrams for Structural Analysis

The different types of stress-strain diagrams available for concrete, according to ACI 318-05 are the following:

User defined
Elastic
PCA parabolic

a) Definition of the elastic stress-strain diagram

The sign criterion for the definition of stress-strain diagram points is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 2 points has been chosen for the definition of the stress-strain diagram. Strain values are the following:

SAε (1)= -1.0E-2
SAε (2)= 1.0E-2

For these points, stress values are the following:

SA σ(i) = SAε (i) · Ex

b) Definition of the PCA parabolic stress-strain diagram

Number of diagram points = 12

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain points have been taken according to notes expressed in ACI-318 article Art. 10.2.6 and are the following:

SDε (1)= -0.0030
SDε (2)= - ε0
SDε (3)= -9/10· ε0
SDε (4)= -8/10· ε0
SDε (5)= -7/10· ε0
SDε (6)= -6/10· ε0
SDε (7)= -5/10· ε0
SDε (8)= -4/10· ε0
SDε (9)= -3/10· ε0
SDε (10)= -2/10· ε0
SDε (11)= -1/10· ε0
SDε (12)= 0.000

Stress points are the following:

If 0 > SAε _(i) > (-SAε 0)

SA σ_(i) = 0.85*fc_t*[2*(SAEPS_(i) /-EPS0)-(SAEPS_(i) /-EPS0)²]

If (-SAε 0) > SA SAε_(i)

SA σ_(i) = 0.85· fc_t

Stress-Strain Diagrams for Section Analysis

The different types of stress-strain diagrams available for concrete, according to the ACI code are the following:

User defined
PCA Parabolic
Rectangular
Linear

a) Definition of the PCA Parabolic diagram

Number of diagram points = 12.

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain points have been taken according to notes expressed in ACI-318 article Art. 10.2.6 and are the following:

SDε (1)= -0.0030
SDε (2)= - -EPS0
SDε (3)= -9/10· ε0
SDε (4)= -8/10· ε0
SDε (5)= -7/10· ε0
SDε (6)= -6/10· ε0
SDε (7)= -5/10· ε0
SDε (8)= -4/10· ε0
SDε (9)= -3/10· ε0
SDε (10)= -2/10· ε0
SDε (11)= -1/10· ε0
SDε (12)= 0.000

The corresponding stress points are the following:

If 0 > SDε_(i) > (-ε0)

SD σ _(i) = 0.85 · fc_t· [2· (SDε_(i) /-ε0)-(SDε_(i) /-ε0)²]

If (-ε0) > SDε

SD σ _(i) = 0.85 · fc_t

b) Definition of the rectangular diagram

Number of diagrams points = 0

Specific points for rectangular diagrams are not defined because stresses do not depend on strains, but on the distance between the outer most compressed fiber and the neutral axis.

c) Construction of the elastic stress-strain diagram

The sign criterion for the definition of stress-strain diagram points is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 2 points have been selected for the construction of the stress-strain diagram. Strain values are the following:

SDε (1)= -1.0E-2
SDε (2)= 1.0E-2

For these points, stress values are the following:

SD σ (i) = SDε (i) · Ex

3. CEB-FIP (Concrete) Properties

CEB-FIP Concrete Properties

βcc

Coefficient which depends on concrete age (Art. 2.1.6.1 (2.1-54))

Used to calculate time-dependant properties:

βcc = exp {s· [1-(28/Age)^1/2]} (Age is expressed in days)

γc

Partial safety factor. (Art. 1.6.4.4)

γc =1.5 (default value) (_c 1)

fck

Characteristic compressive strength (Art. 2.1.3.2)

Depends on concrete age:

fck_t = fcm_t - 8 (in MPa) (+Compression)

fcd

Design compressive strength (Art. 1.4.1 b)

Depends on concrete age:

fcd_t = fck_t/γc (+Compression)

fcd1

Uniform strength for uncracked regions (Art. 6.2.2.2)

Depends on concrete age:

fcd1 = 0.85· (1-fck_t/250) ·fcd_t (fcd1, fck_t and fcd_t in N/mm²)

fcd2

Uniform strength for cracked regions (Art. 6.2.2.2)

Depends on concrete age:

fcd2 = 0.60 · (1-fck_t/250) ·fcd_t (fcd2, fck_t and fcd_t in N/mm²)

fcm

Mean compressive strength (Art. 2.1.6.1 (2.1-53))

Depends on concrete age:

fcm_t = βcc · fcm_28-day (+Compression)

fctm

Mean tensile strength (Art. 2.1.3.3.1 (2.1-4))

fctm = 1.40 · [(fck/10)^2/3] (fctm and fck in N/mm²) (+ Tension)

fctk min

Lower characteristic tensile strength (Art. 2.1.3.3.1 (2.1-2))

fctk_min = 0.95 · [(fck/10)^2/3] (fctk_min and fck in N/mm²) (+ Tension)

fctk max

Upper characteristic tensile strength (Art. 2.1.3.3.1 (2.1-3))

fctk_max = 1.85 · [(fck/10)^2/3] (fctk_max and fck in N/mm²) (+ Tension)

Cement type

Type of cement (appendix d.4.2.1)

S:	Slow hardening cements
N:	Normal hardening cements (default value)
R:	Rapid hardening cements
RS:	Rapid hardening high strength cements

εc1

Strain of the peak compressive stress (Art. 2.1.4.4.1)

εc1 = - 0.0022 (-Compression)

εcuB

Maximum strain in bending for parabolic rectangular diagram (Art. 6.2.2.2 (6.2-2)). This strain varies with the concrete characteristic strength, following the criteria specified bellow: (+ Compression)

If fck 50 (in MPa)		εcuB = 0.0035
If fck 50 (in MPa)		εcuB = 0.0035· (50/fck) (in N/mm²)

εcuC

Maximum strain in compression for parabolic rectangular diagram (Art. 6.2.2.2 (6.2-6))

εcuC = 0.0035 (+ Compression)

εcuU

Maximum strain for uniform stress diagram (Art. 6.2.2.2 (6.2-6))

εcuU = 0.004 - 0.002· (fck/100) (in N/mm²) (+Compression)

εc lim.

Maximum strain in compression (Art. 2.1.4.4.1)

Eci

Tangent modulus of elasticity (Art. 2.1.4.2)

Depends on concrete age:

Eci = βcc^1/2· 2.15E4 · {[(fcm_t)/10]^1/3} (in N/mm²)

Reduced modulus of elasticity (Art. 2.1.4.2)

Depends on concrete age:

Ec = 0.85 · Eci

Ec1

Secant modulus of elasticity (Art. 2.1.4.4.1)

Depends on concrete age:

Ec1 = βcc^1/2 ·fcm_t/(- εc1)

Stress-Strain Diagrams for Structural Analysis

The different types of stress-strain diagrams available for concrete, according to CEB-FIP code are the following:

User defined
Elastic
Instantaneous loading

a) Definition of the elastic stress-strain diagram

The sign criterion for the definition of stress-strain diagram points is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 2 points has been chosen for the definition of the stress-strain diagram. Strain values are the following:

SAε (1)= -10^-2
SAε (2)= 10^-2

For these points, stress values are the following:

SA σ(i) = SAε (i) · Ex

b) Definition of the Instantaneous loading stress-strain diagram

Number of diagram points = 20

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain point values conform to article Art. 2.1.4.4.1 and are the following:

SAε (1)= 1.000 · (εcu-εc1)+ εc1
SAε (2)= 0.793 · (εcu-εc1)+ εc1
SAε (3)= 0.617· (εcu-εc1)+ εc1
SAε (4)= 0.468· (εcu-εc1)+ εc1
SAε (5)= 0.342· (εcu-εc1)+ εc1
SAε (6)= 0.234· (εcu-εc1)+ εc1
SAε (7)= 0.143· (εcu-εc1)+ εc1
SAε (8)= 0.066· (εcu-εc1)+ εc1
SAε (9)= 1.000 · εc1
SAε (10)= 0.964· εc1
SAε (11)= 0.922· εc1
SAε (12)= 0.873· εc1
SAε (13)= 0.816· εc1
SAε (14)= 0.749· εc1
SAε (15)= 0.669· εc1
SAε (16)= 0.575· εc1
SAε (17)= 0.465· εc1
SAε (18)= 0.335· εc1
SAε (19)= 1.181· εc1
SAε (20)= 0.000

The corresponding stress values are:

SA σ _(i)= [((Eci/Ec1* SAε_(i)/ εc1)-( SAε S_(i)/ εc1)²)/(1+(Eci/Ec1-2)* ε_(i)/ εc1)]*fcm_t

Stress-Strain Diagrams for Section Analysis

The different types of stress-strain diagrams available for concrete, according to CEB-FIP code are the following:

User defined
Parabolic rectangular
Uniform stress

a) Definition of the parabolic rectangular diagram

Number of diagram points = 12

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain point values conform to article Art. 6.2.2.2 and are the following:

SDε (1)= -cuB
SDε (2)= c1
SDε (3)= -9/10· c1
SDε (4)= -8/10· c1
SDε (5)= -7/10· c1
SDε (6)= -6/10· c1
SDε (7)= -5/10· c1
SDε (8)= -4/10· c1
SDε (9)= -3/10· c1
SDε (10)= -2/10· c1
SDε (11)= -1/10· c1
SDε (12)= 0.000

The corresponding stress point values are the following:

If SD_(i) > c1

σ_(i) = -0.85 · fcd_t · [2*(SD_(i) /-c1)+(SD_(i) /-c1)²]

If SD_(i) < c1

σ_(i) = -0.85 · fcd_t

b) Definition of uniform stress stress-strain diagrams

Number of diagram points = 3

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain point values conform to article Art. 6.2.2.2 and are the following:

SD (1)= -c1
SD (2)= -c1/1000
SD (3)= 0.000

The corresponding stress point values are the following:

SDσ (1)= -fcd2
SDσ (2)= -fcd2
SDσ (3)= 0.00

4. EHE (Concrete) Properties

EHE Concrete Properties

γc

Partial safety factor (Art. 15.3)

γc =1.5 (default value) (_c 1)

βc

Coefficient which depends on concrete age (Art. 30.4)

Used to calculate time-dependant properties:

βc = exp {K · [1-(28/Age)^1/2]} (Age is expressed in days)

Coefficient (0 K 1) which depends on the type of cement used. The value of this factor can be found in Annex 13 of the EHE-1998 and in 31.3 in the EHE-2008, which states the following:

CeTp = N	K = 0.25
CeTp = R	K = 0.20
CeTp = S	K = 0.38

Cement type

Type of cement. The different types of cement are described in article Art. 30.4 and are the following:

N	Normal hardening cements (default value)
R	Rapid hardening cements
S	Slow hardening cements

fck

Characteristic compressive strength (Art. 39.6)

Depends on concrete age:

fck_j = fck · βc (N/mm²) (+Compression)

fcm

Mean compressive strength (Art. 39.6)

Depends on concrete age:

fcm_j = fck_j + 8 (N/mm²) (+Compression)

fcd

Design compressive strength (Art. 39.4)

Depends on concrete age:

fcd_t = fck_t/γc (+Compression)

ßt

Coefficient which depends on concrete age. Used to calculate time-dependant properties (Art. 30.4)

βt= exp {0.10 · [1-(28/Age)]} (Age is expressed in days)

fctm

Mean tensile strength (Art. 30.4)

Depends on concrete age:

fctm_j = fctm · βt

fctm = 0.3 · (fck^2/3) (N/mm²)

fctk005

Lower characteristic tensile strength (percentile-5%) (Art. 39.1)

fctk_005 = 0.21· (fck^2/3) (N/mm²) (+ Tension)

fctk095

Upper characteristic tensile strength (percentile-95%) (Art. 39.1)

fctk_095 = 0.39 · ( fck^2/3) (N/mm²) (+ Tension)

εc1

Strain of the peak compressive stress (Art. 21.3.3)

εc1= 0.0022 (default value) (+ Compression)

εc lim.

Ultimate strain in compression (Art. 21.3.3 Table 21.3.3)

εc lim 0

According to CEB-FIP, Art. 2.1.4.4.1:

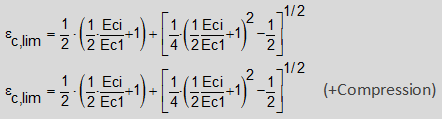Eci

Tangent modulus of elasticity (Art. 21.3.3 Table 21.3.3) (Eci 0)

According to the Art. 2.1.4.4.1 of the CEB-FIP code

Eci=2.15· ((fcm/10)^1/3) (in MPa)

Secant modulus of elasticity (Art. 39.6)

Depends on concrete age:

Ej = βc^1/2 · 8500 · (fcm_j^1/3) (N/mm²)

Initial modulus of elasticity (Art. 39.6)

Depends on concrete age:

E0 = βc^1/2 ·10000 · (fcm_j^1/3) (N/mm²)

Stress-Strain Diagrams for Structural Analysis

The different types of stress-strain diagrams available for concrete, according to EHE code are the following:

User defined
Elastic
Instantaneous loading

a) Definition of the elastic stress-strain diagram

The sign criterion for the definition of stress-strain diagram points is as follows:

Positive (+) Tension, Negative (-) Compression

A total of 2 points has been chosen for the definition of the stress-strain diagram. Strain values are the following:

SAε (1)= -10^-2
SAε (2)= 10^-2

For these points, stress values are the following: .

SAσ(i) = SAε(i) · Ex

b) Definition of the instantaneous loading stress-strain diagram

Number of diagram points = 20

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain point values conform to article Art. 21.3.3 and are the following:

SAε (1)= - εc lim
SAε (2)= -0.793 · (εc lim- εc1)- εc1
SAε (3)= -0.617· (εc lim- εc1)- εc1
SAε (4)= -0.468· (εc lim- εc1)- εc1
SAε (5)= -0.342· (εc lim- εc1)- εc1
SAε (6)= -0.234· (εc lim- εc1)- εc1
SAε (7)= -0.143· (εc lim- εc1)- εc1
SAε (8)= -0.066· (εc lim- εc1)- εc1
SAε (9)= - εc1
SAε (10)= -0.964· εc lim
SAε (11)= -0.922· εc lim
SAε (12)= -0.873· εc lim
SAε (13)= -0.816· εc lim
SAε (14)= -0.749· εc lim
SAε (15)= -0.669· εc lim
SAε (16)= -0.575· εc lim
SAε (17)= -0.465· εc lim
SAε (18)= -0.335· εc lim
SAε (19)= -0.181· εc lim
SAε (20)= 0.000

The corresponding stress points are the following:

SAσ_(i)= -[(k·η_(i)- η_(i)²)/(1+(k-2) · η)]*fcm_j

Where:

K = Eci·εc1/(fcm_28-day)
η_(i) = -SAε_(i)/ εc1

Stress-Strain Diagram for Section Analysis

The different types of stress-strain diagrams available for concrete, according to the EHE code are the following:

User defined
Parabolic rectangular
Bilinear
Rectangular

a) Definition of the parabolic rectangular stress-strain diagram

Number of diagram points = 12

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain point values conform to article Art. 39.5 a) and are the following:

SDε (1)= -εmin
SDε (2)= -εint
SDε (3)= -9/10· int
SDε (4)= -8/10· int
SDε (5)= -7/10· int
SDε (6)= -6/10· int
SDε (7)= -5/10· int
SDε (8)= -4/10· int
SDε (9)= -3/10· int
SDε (10)= -2/10· int
SDε (11)= -1/10· int
SDε (12)= 0.000

The corresponding stress points are the following:

EHE-98

For the first 11 points:

SD σ _(i) = 1000*SDε_(i) *[250*SDε_(i) +1]*0.85*fcd_j

For point 12:

SD σ _(i) = 0.85*fcd_j

EHE-08

For the first 11 points:

SD σ _(i) = fcd_j*[1-(1-SDε_(i) / εint)ⁿ]

n = 2; fck 50 MPa

n =1.4 + 9.6 * [(100-fck)/100]⁴; fck > 50 MPa

For point 12:

SD σ_(i) = fcd_j

b) Definition of the bilinear stress-strain diagram

Number of diagram points = 3

The sign criterion for the definition of points of the stress-strain diagram is as follows:

Positive (+) Tension, Negative (-) Compression

Strain point values conform to article Art. 39.5 a) and are the following:

SDε (1)= - εmin
SDε (2)=- EPSint
SDε (3)=0.000

The corresponding stress points are the following:

EHE-98

SDσ (1)= -0.85*fcd_j
SDσ (2)= -0.85*fcd_j
SDσ (3)= 0.00

EHE-08

SDσ (1)= fcd_j
SDσ (2)= fcd_j
SDσ (3)= 0.00

c) Definition of the rectangular stress-strain diagram

Number of diagram points = 0

Specific points for rectangular diagrams are not defined because stresses do not depend on strains, but on the distance between the outer most compressed fiber and the neutral axis.

The contents of Concrete Material

Cracking in concrete

Creep and Shrinkage