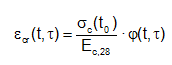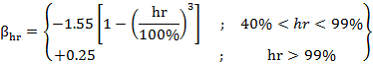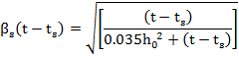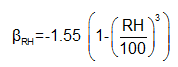Shrinkage and creep are long term time-dependent effects and can cause strains and displacements that can change forces, stresses, reactions or the prestress load which the structure is subjected to.
Shrinkage is an unloaded time-dependent deformation, while creep is an under load time-dependent deformation. Although both concepts are two aspects of a single complex physical phenomenon, based on the reological behavior of concrete, they should be considered as independent and studied separately.
Time-dependent deformation of a concrete member under constant stress (ignoring thermal expansion) is computed as:
where:
|
|
Instant elastic strain
|
|
|
Creep strain at age t
|
|
|
Shrinkage strain at age t
|
Elastic and creep strains are stress-dependent and are usually considered together and shrinkage strain separately.
One of the hypothesis in the study of creep is linearity, means that strain is proportional to stress:
where:
|
|
Creep strain at time t under a constant stress applied at
|
|
|
Constant stress applied at time
|
|
|
Elasticity modulus at 28 days
|
|
|
Creep coefficient
|
Therefore, stress-dependent strain may be estimated from:
|
|
Elasticity modulus at loading age
|
|
|
Creep function
|
Validity of linearity hypothesis is experimentally confirmed for initial stresses not greater than 40% of concrete mean compressive strength.
Another hypothesis commonly accepted is the superposition principle, which says that the strain produced in concrete at any time t by any increase of stress applied in time , is independent from any increase of stress produced before or after .
So, defining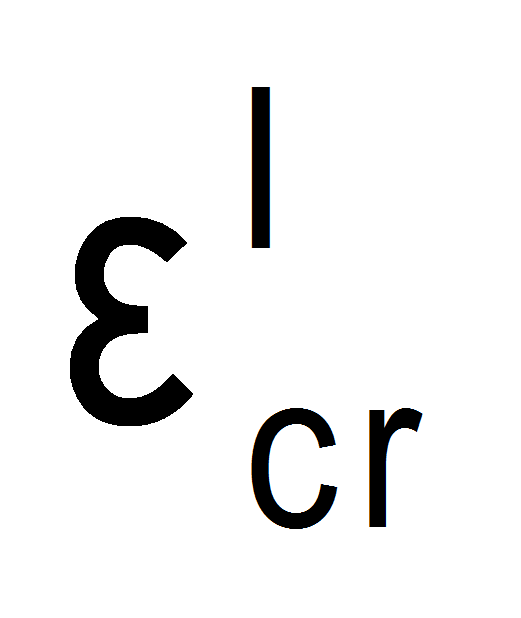 
as the strain produced by a load applied in 1 and 
as the strain produced in a time 
, as result of both loads:
Creep strains are, therefore, addable, so the total strain of concrete for a history of variable loads should be:
Shrinkage analysis method
Shrinkage in CivilFEM is computed from shrinkage strain curves defined in concrete materials. These curves are calculated from the available codes in the program or can be defined point by point. The curves related shrinkage strains with concrete material age.
Shrinkage strains will be computed in all materials activated with this option. They are introduced in the model by temperature increments and calculated from strain and thermal expansion coefficient of the material.
Creep analysis method
For the calculation of the integral explained in the previous chapter (analysis in time of a structure subjected to creep), CivilFEM uses the step by step standard method.
In the step by step method the time is divided into a series of intervals, so that in each of the intervals the equilibrium and compatibility conditions of the structure are satisfied.
The solution procedure of CivilFEM employs a non linear calculation with the time discretization. Strain increments produced by creep are computed from creep coefficients defined in the material and from stress increments produced during time discretization:
Because total equivalent (J2) stress (always positive) is used to calculate step by step increments, no changes in the stress sign (positive to negative stresses, or vice versa) are necessary to have correct evaluation of creep.
Creep and Shrinkage codes
1. EHE-98 (Spanish code)
In this code the creep coefficient may be calculated from:
Where, 0 is the notional creep coefficient and c is a coefficient to describe the development of creep with time after loading, t is the age of concrete in days at the considered moment and t0 the age of concrete at loading in days:
where:
is a factor to allow for the effect of relative humidity on the notional creep coefficient.
is a factor to allow for the effect of concrete strength on the notional creep coefficient and fck is the characteristic compressive strength.
is a factor to allow for the effect of concrete age at loading on the notional creep coefficient.
is the notional size of member in millimetres, where Ac is the cross section and u is the perimeter of the member in contact with the atmosphere ( this value must be introduced by the user).
The coefficient for the development of creep with time may be estimated from:
Where (t-0 ) is the non-adjusted duration of loading in days and H is a coefficient depending on the relative humidity (RH in %) and the notional member size h0 (mm).
The shrinkage or swelling strains may be calculated from:
where:
|
sh0
|
Notional shrinkage coefficient
|
|
s
|
Coefficient to describe the development of shrinkage with time
|
|
t
|
Age of concrete in days
|
|
ts
|
Age of concrete in days at the beginning of shrinkage
|
The notional shrinkage coefficient may be obtained from:
with:
s = (570 – 5 fck) 10-6
fck is the characteristic compressive strength (N/mm2 )
Open air structures (RH<100%):
Submerged structures:
|
RH
|
Relative humidity
|
|
s(t-ts)
|
Coefficient for shrinkage development with time
|
2. Eurocode 2 (ENV 1992-1-1:1991)
In this code the creep coefficient is calculated as:
Where, 0 is notional creep coefficient and c coefficient to describe the development of creep with time after loading, t is the age of concrete in days at the moment considered and t0 the age of concrete at loading in days:
Where:
is a factor to allow for the effect of relative humidity on the notional creep coefficient.
is a factor to allow for the effect of concrete strength on the notional creep coefficient.
is a factor to allow for the effect of concrete age at loading on the notional creep coefficient.
is the notional size of member in millimeters where Ac is the cross section and u is the perimeter of the member in contact with the atmosphere (this value must be introduced by the user).
The coefficient c for the development of creep with time may be estimated from:
Where (t-0) is the non-adjusted duration of loading in days and H is a coefficient depending on the relative humidity (HR in %) and the notional member size h0 (mm):
The shrinkage or swelling strains may be calculated from:
where:
|
cs0
|
Notional shrinkage coefficient
|
|
s
|
Coefficient to describe the development of shrinkage with time
|
|
t
|
Age of concrete in days
|
|
ts
|
Age of concrete in days at the beginning of shrinkage
|
The notional shrinkage coefficient may be obtained from:
where
where sc is a coefficient which depends on type of cement:
-
4 for slowly hardening cement (S)
-
5 for normal (N) or rapid hardening (R) cements
-
8 for rapid hardening high strength cements (RS).
The coefficient for the development of shrinkage with time may be estimated from:
Where:
|
h0
|
Notional size in millimeters 
|
|
Ac
|
Cross section area
|
|
u
|
Perimeter of the member in contact with the atmosphere
|
|
(t-ts)
|
Actual non-adjusted duration of shrinkage in days
|
3. Eurocode 2 (EN 1992-1-1:2004/AC:2008)/ EHE-08 (Spanish code)
In this code the creep coefficient may be calculated from:
Where, 0 is the notional creep coefficient and c is a coefficient to describe the development of creep with time after loading, t is the age of concrete in days at the considered moment and t0 the age of concrete at loading in days:
where:
if
.
if
is a factor to allow for the effect of relative humidity on the notional creep coefficient.
is a factor to allow for the effect of concrete strength on the notional creep coefficient and fck is the characteristic compressive strength.
is a factor to allow for the effect of concrete age at loading on the notional creep coefficient.
is the notional size of member in millimetres, where Ac is the cross section and u is the perimeter of the member in contact with the atmosphere ( this value must be introduced by the user).
The coefficient for the development of creep with time may be estimated from:
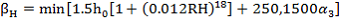if
if
Where (t-0 ) is the non-adjusted duration of loading in days and H is a coefficient depending on the relative humidity (RH in %) and the notional member size h0 (mm).
The shrinkage or swelling strains may be calculated from:
is the total shrinkage strain
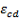is the drying shrinkage strain
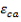is the autogenous shrinkage strain
The development of the drying shrinkage strain in time follows from:
Where:
Values for 
are interpolated with the table:
|
|
|
|
100
|
1.0
|
|
200
|
0.85
|
|
300
|
0.75
|
|
≥500
|
0.70
|
Submerged structures:
Where:
is the mean compressive strength(MPa)
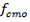= 10 MPa
are coefficients which depends on the type of cement
= 3 for cement Class S
= 4 for cement Class N
= 6 for cement Class R
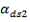= 0.13 for cement Class S
= 0.12 for cement Class N
= 0.11 for cement Class R
RH is the ambien relative humidity (%).
The autogenous shrinkage strain follows from:
Where:
4. American Code ACI 209R-92
This code defines creep coefficient through a monomial equation which includes the influence of different factors:
The average value suggested for and PSI is = 2.35, PSI = 0.6.
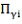are correction factors for conditions other than the standard concrete conditions: loading age, volume-surface ratio method, ambient relative humidity, etc.
The equation for shrinkage deformation in ACI code is similar to the equation for creep:
The average value suggested for R and α is R = 780 , α=1
In the same way as for the creep model I are correction factors for conditions other than the standard concrete conditions: volume-surface ratio method, ambient relative humidity, etc.
CEB_FIP 90 Model Code
In this code the creep coefficient is calculated as:
Where, 0 is the notional creep coefficient and c coefficient to describe the development of creep with time after loading, t is the age of concrete in days at the moment considered and t0 the age of concrete at loading in days:
Where:
is a factor to allow for the effect of relative humidity on the notional creep coefficient.
is a factor to allow for the effect of concrete strength on the notional creep coefficient.
is a factor to allow for the effect of concrete age at loading on the notional creep coefficient.
Where h0 is the notional size in mm 
, Ac describes the cross section area, u is referred to the perimeter of the member in contact with the atmosphere and, by last, fcm means the compressive strength of concrete at the age of 28 days (MPa).
The coefficient c for the development of creep with time may be estimated from:
Where (t-0 ) is the non-adjusted duration of loading in days and H is a coefficient depending on the relative humidity (HR in %) and the notional member size h0 (mm):
The shrinkage or swelling strains are calculated as:
where:
|
cs0
|
Notional shrinkage coefficient
|
|
s
|
Coefficient to describe the development of shrinkage with time
|
|
t
|
Age of concrete in days
|
|
ts
|
Age of concrete in days at the beginning of shrinkage
|
The notional shrinkage coefficient may be obtained from:
with
where sc is a coefficient which depends on type of cement:
-
4 for slowly hardening cement (S)
-
5 for normal (N) or rapid hardening (R) cements
-
8 for rapid hardening high strength cements (RS).
The coefficient for the development of shrinkage with time may be estimated from:
Where:
|
h0
|
Notional size in mm. 
|
|
Ac
|
Cross section area
|
|
u
|
Perimeter of the member in contact with the atmosphere
|
|
(t-ts)
|
Actual non-adjusted duration of shrinkage in days
|
